This week we're continuing our unit on sketching polynomials and, I have to say, it's shaping up to be one of my favorite units this year. My students have always struggled with math, so seeing them able to sketch these "complicated looking functions" has been pretty awesome.
First, I gave out this graphing polynomials cheat sheet as an overview of what the graphs would look like and the terminology we'd be using in class (you can find more about this reference here).
We also talked about how we'd be graphing backwards, starting with the end behavior and snaking backwards through the zeros. With this technique, students wouldn't have to memorize each degree graph's shape.
This example of a polynomial graph is part of our Algebra 2 word wall. My students refer to it a lot. Having an example that is always on the wall is a great way for students to make connections between polynomial graphs and their equations and what makes a graph bounce or cross the x axis. I also love that I always have an example to point to when we are taking notes or when a student is struggling with an independent work problem.
We also sketched this little chart on which ways a graphs arrows should point depending on its degree. It's a good way to check work.
From the very first day, we used this polynomial quick check template for warm ups and extra practice of polynomials that I wrote on the board.
On the very first day before introducing the information above, I gave my students a quick check sheet and a quadratic in factored form to graph. We then had something familiar to compare our new graphs to. We compared the graphs' zeros and remembered that we plot opposite of what the number is inside parenthesis.
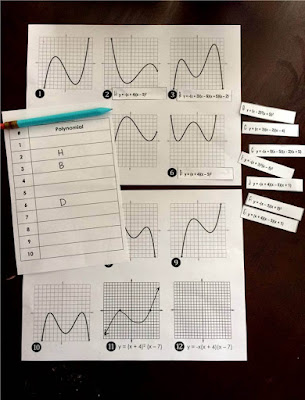
Before we got into more open-ended graphing questions, I gave my students this quick polynomial matching activity. I find that matching activities are great confidence-boosting ice breakers, especially with tough topics.
After the matching activity, I gave my students a few polynomial equations, a few quick check sheets and asked them to find the degree, end behavior, zeros, if there were any multiplicities, and to sketch the graph. We did some more practice with various degree polynomials, ones that we first had to factor, and ones with multiplicities greater than 2.
Today we talked about how a f(x)=(x + 2)^2 graph would look very similar to a f(x)=(x + 2)^4 graph, because of the even multiplicities.
As much as I'd like to spend weeks (months) on sketching polynomials, we needed to sum up. In addition to a quiz, I gave this 28-question set of sketching polynomials task cards to sum up our unit. 16 of the cards ask students to sketch and the other 12 ask them to write the equations of given graphs.
 |
| Algebra 2 Activities Bundle |
I also made this reference sheet for the steps of polynomial long division.
We use this synthetic division reference sheet in my inclusion Algebra 2 class to help our students remember the steps. They are usually good with using the Quadratic Formula to find the nonreal zeros, so that step isn't shown.











This is AMAZING!! This is one of my favorite units to teach as well. These items are a great way to put everything together in one place. Thank you so much!
ReplyDeleteIt's such a fun unit!
DeleteDo you allow them to find the zeros using their graphing calculators in these activities?
ReplyDeleteIn our quadratics unit, yes. In our polynomials unit students sketch given the equation so don't need their graphing calculators. When synthetic division is necessary to find imaginary zeros, they use their graphing calculators to find the real zero then find the other zeros with the algorithm.
DeleteYou are so creative. I love the math word wall and the unit circle. Thank you for coming up with ideas for Algebra 2. Well Done!
ReplyDeleteThank you! I wish I knew your name to thank you personally. I hope you are having a great year:)
Delete