This week, my Algebra 2 students started factoring. We started with a Let's Factor! Powerpoint with no trinomials in sight- just a bunch of thinking questions like "What 2 numbers multiply to 6 and add to 7?". My students responded really well to this introduction and they were so much more open to the idea of factoring quadratics after getting this confidence boost.
This year I made factoring a whole lot less abstract and it's been amazing to see and hear all the exclamations of "Oh, I get it now!" Isn't this what every Math teacher lives for? So here is how I plan to tackle factoring and the reasons it is hard:
Reason 1: Multiplication facts
The first reason my students have trouble factoring is because of the multiplication. "What 2 numbers multiply to 12 that add to 7?" My students get stuck on the multiply to 12 part. To get around this, I went for it this year. I handed out little multiplication charts.
For years I've wanted to hand them out but didn't want to embarrass my students. But after one of my more self-conscious students thanked me for the chart this year, I knew I made the right choice. Here's our chart:
The only important numbers are those in green and yellow. The green ones will make factoring differences of squares a little easier later on. The red ones are primes (highlighting these is just cool). The grey ones are duplicates so we can just toss those right out. See, it's already easier!
Reason 2: Abstractness
The second reason factoring is so hard for my students is because it is so abstract. It goes backwards. Just like subtraction and division are harder than addition and multiplication, factoring is harder than distributing. To tackle the abstractness, we went all-in hands-on this year to start our unit.
We started our factoring with the "Let's Factor!" PowerPoint. Since most of my students struggle with multiplication, I wanted to turn factor finding into something fun at first and less mathy. The first few slides look like the one above. The green "check your answer" boxes click to the correct factor pairs- fun! After a few rounds, the kids got a taste of the thinking needed to factor. They wanted to figure out these little puzzlers and had no idea they were factoring.
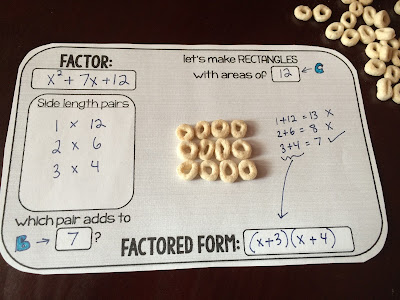
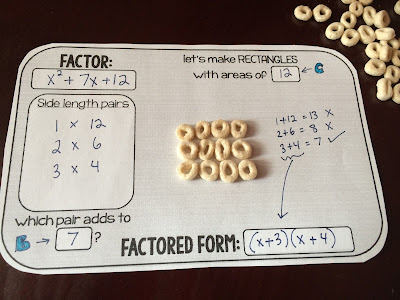
Next, we went very hands-on with... Cheerios!
This is a little factoring mat I made to make factoring less abstract. Every student got a few half sheets and a bag of cereal. We filled in the FACTOR, "B" and "C" boxes together. I figure Cheerios are a low-allergy food (I'm so paranoid about that!) so they'll be safe and a lot cheaper and more accessible than Algebra tiles.
In this problem, students needed to find as many rectangles as they could with an area of 12 [Cheerios] and record the side lengths. Easy, right? So which pair adds to 7?
Oh, 3 and 4 add to 7? Well then, you just factored! Awesome job!
Before introducing negative numbers in our trinomials, we summarized understanding and learning with a 10-question zooming Prezi. I recently learned how to use my iPhone as a Prezi clicker so was feeling super cool advancing the slides from my phone. The kids weren't very impressed:)
After the Prezi we began our simplified factoring notes. It really helped to break factoring down and cover a new type of trinomial each day. I didn't introduce any negative numbers until day 3.
And to show off what we know, we'll decorate our classroom with these fun pennants:)
My students are going to work hard this unit. It's a struggle every year, but when they get it, it's a great feeling both for them and for me. There's nothing better and it's the biggest reason I love teaching Special Education. It's awesome.
More factoring ideas can be found in the post Fun with Quadratics.











I LOVE the way you introduce factoring by having students factor without knowing they are factoring. Do you have a copy of your powerpoint "let's factor" available for download or purchase in your TPT Store?
ReplyDeleteThanks!
Thank you for posting this because I see I had referenced it and then it was nowhere to be found! I just put it up in my TpT store/ You can download it for free at this link: http://bit.ly/1MbTgdH I need more sleep! :)
DeleteDon't we all?! :) Thanks so much! I am excited to use it next chapter!
DeleteHonestly I haven't had much issue with factoring when the l as coefficient is one. The trouble starts when the lead is greater than one. Any suggestions?
ReplyDeleteI love the way you introduce factoring, very creative.
Thank you in advance for any input.
The way that has worked for my students is the AC method. We find the factors of AC that add to B, replace B with the factors, then factor by grouping. I have a reference sheet for the method in my dropbox in the sidebar.
DeleteCheck out the magic X, it's easier for my students, the don't dread factoring even when a is not 1.
ReplyDelete