The first thing I hear when telling people I teach Algebra 2 is, "Whoa, that must be hard!", or something along these lines. If you teach high school, you know that high school kids are just little kids in big bodies who usually have even bigger emotions. But I have found that they sometimes like to hide these emotions deep, deep down and that this is especially true in math.
What I want to tell people when they ask what I do for a living is "boost kids' feelings towards Math". Can I make that an official title? All jokes aside, I take this part of my job very seriously. Word walls in my classroom are an essential extension of my teaching. Kids say the darndest things! They also ask the most random questions. And when they do, I am able to quickly point at a reference on our math word wall.
So what is on our word wall? Well it's grown a lot since I first started adding math references to our classroom walls. Below are the 4 most important things I feel should be included on an Algebra 2 word wall.
1: Anchor chart examples
Something I recently learned is that people need to develop the skill of using an example to complete a similar problem. I had assumed everyone just did this naturally. It makes a lot of sense.
Confidence seems to increase when students can more independently use examples to complete new problems. I have found that example posters help.
Here are a couple posters I painted that act as examples for factoring trinomials and binomials. That factoring binomials is so much harder for students may always remain a mystery!
On our word wall are references for domain, range, increasing and decreasing with notation references and then graph examples for increasing and decreasing.
In Algebra 2, we shift functions all year. Having vertex-form anchor charts in my classroom totally transformed my ability to teach Algebra 2. When those little questions come up about whether x shifts left or right, I can quickly remind students by pointing to an example.
Especially during our quadratics unit, keywords are so important. This Quadratic Keywords poster helps to make our projectile motion unit one of my favorite units to teach. It's fun for me to see how much progress my students make during this unit, and it's fun for them to be able to solve equations that a week earlier seemed impossible.
My students have made the following observations about Quadratic, Radical and Absolute Value functions:
"Curvy brackets, curvy graph." (Quadratic)
"The radical graph looks like the square root symbol." (Radical)
"The lines are straight just like the sides of the graph." (Absolute Value)
Connecting the keywords back to contextualized examples lets students see how these words are used in the math. To me, this works a whole lot better than using a math word wall as a dictionary.
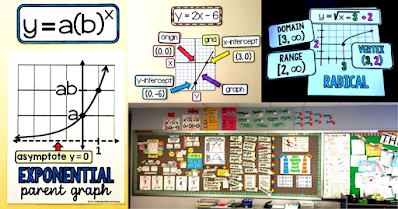
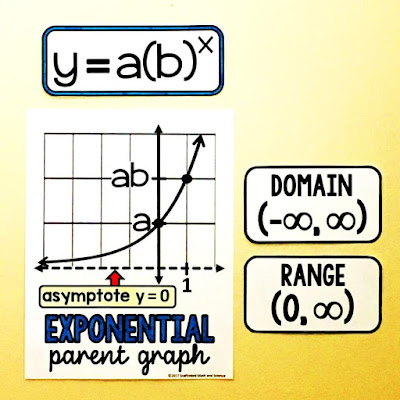
2: Parent graphs and equations
Here is an awesome photo math teacher and Instagrammer @ffalaknaazz sent. I had been guilty of not photographing every math word wall update and these parent graphs fell into that category. I'm pretty thankful for this photo.
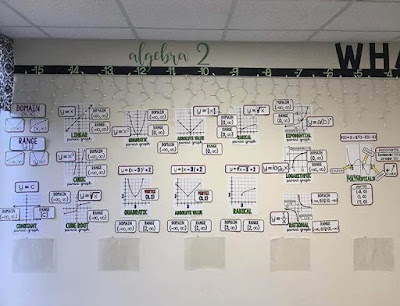 |
| Algebra 2 Word Wall |
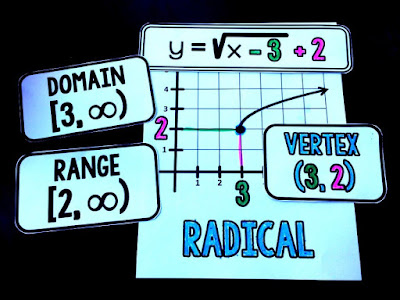
Parent graphs let students see the shape of the graphs we will see in class along with their domain and range and equation form.
And of course, equations. Here is our Quadratic Formula poster.
Once I added the white paint (ok, the whiteout) to the variables, my students were better able to add in their values to solve.
3: Links back to Algebra 1
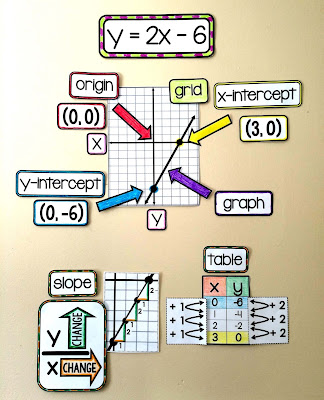
The year before I added an Algebra 1 section to our Algebra 2 word wall, I must have drawn a linear graph on the board 200 times to link back to what my students had already learned a couple years earlier.
I'd draw a line, mark its x-intercept and ask what the y value at that x-intercept was so that we could link this prior knowledge to finding zeros during our quadratics unit. I'd point to that straight line and ask what the x value at the y-intercept was when we were discussing the C value in our quadratic word problems. We'd look at slope and make connections to the A value in absolute value function graphs.
There were so many times I needed that linear reference that I eventually made it a permanent part of our room.
4: A little inspiration
Of all the classes I have taught, Algebra 2 is the class where I have seen the most student growth from the beginning of the year to the end. Students come into our abstract Algebra 2 class from the concrete Geometry class they finished up a couple months earlier not really knowing what to expect. They're a little nervous from hearing their friends say how hard Algebra 2 is. Some just want to get it out of the way.
This Sylvia Duckworth poster hangs on the old TV in my room. I point it out to the kids and also like to look at it for myself. It is just so perfect.
Just about everyone struggles at first, but by even just a few weeks in students start seeing the common pattern in vertex form functions and how to make a solid table from which to graph, and things start to click. It's amazing to see how much students grow to be able to do in Algebra 2. I love the course so much for this.
But it's not all sunshine and roses for everyone! Some students actually sweat Algebra 2 big time. And by sweat I mean physically sweat. A lot. It can be a stressful course, which is where math word walls and math cheat sheets come in. Given that the dropout rate has been correlated to forcing kids to take Algebra 2, all of them can use a little inspiration.
 |
| High School Math Word Wall Ideas |
Every year I add more and more to our word walls. The post High School Math Word Wall Ideas has additional photos of the word walls in our classroom.
More math word wall posts:







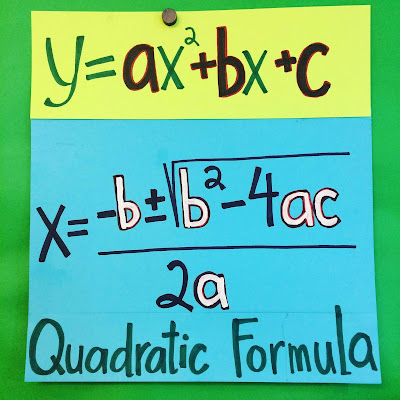



Fantastic Post!! We (math teachers at my school) are always looking for word wall ideas that are not boring! GREAT JOB!
ReplyDeleteThank you so much for letting me know (and for reading my post at all - lol!) :)
DeleteHello, I am a certified Biology and English teacher who, because I also have the hours in math, am teaching Algebra II and Geometry at a small high school that has been without a math teacher for 2 years. In addition to catching up the nonsped students, I need to reach the sped ones, too. This post is great, but my experience with some of the sped students is that their processing skills are not up to the task even if working one on one with them for large amounts of time each day. Do you have a suggestion for modifying the curriculum in a way that they get the basics and can master them on their own? Thanks!
ReplyDeleteI am a big believer in math word walls because the information stays available for students even when we are not on that topic. The references help keep prior learning activated and let students be a bit more independent. In my Algebra 2 classroom there are word wall references for Algebra too to help my students relate new material back to what they had previously learned. On my blog is also a post called "4 FREE Algebra and Algebra 2 Warm-up Templates". We use these templates for warm ups and quick checks a lot. The template becomes a familiar routine.
DeleteBut more than anything, I feel that it could be a lack of confidence. This is what I see in my own students. I'd maybe even say this is most of it. If a kid appears to be processing slowly there could be an emotional component there. Our kids have failed repeatedly, so math is scary. I know that I shy away from things that I don't like, and I don't like things that I have failed at. So it becomes a "which came first?" situation. In my experience, word walls, routine and encouragement go a long way. And jokes! I like to keep things light.